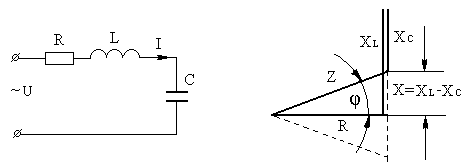
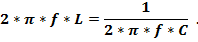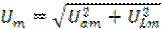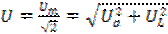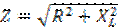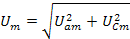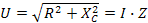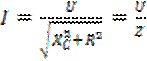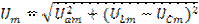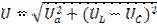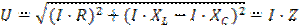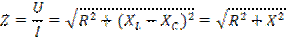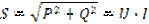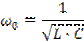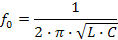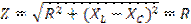Электрическая цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром.
Принимаем фазу тока нулевой, т.е. ток в этой цепи изменяется по закону: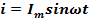 
.
Тогда напряжение на активном сопротивлении будет изменяться как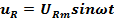 
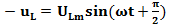
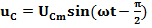
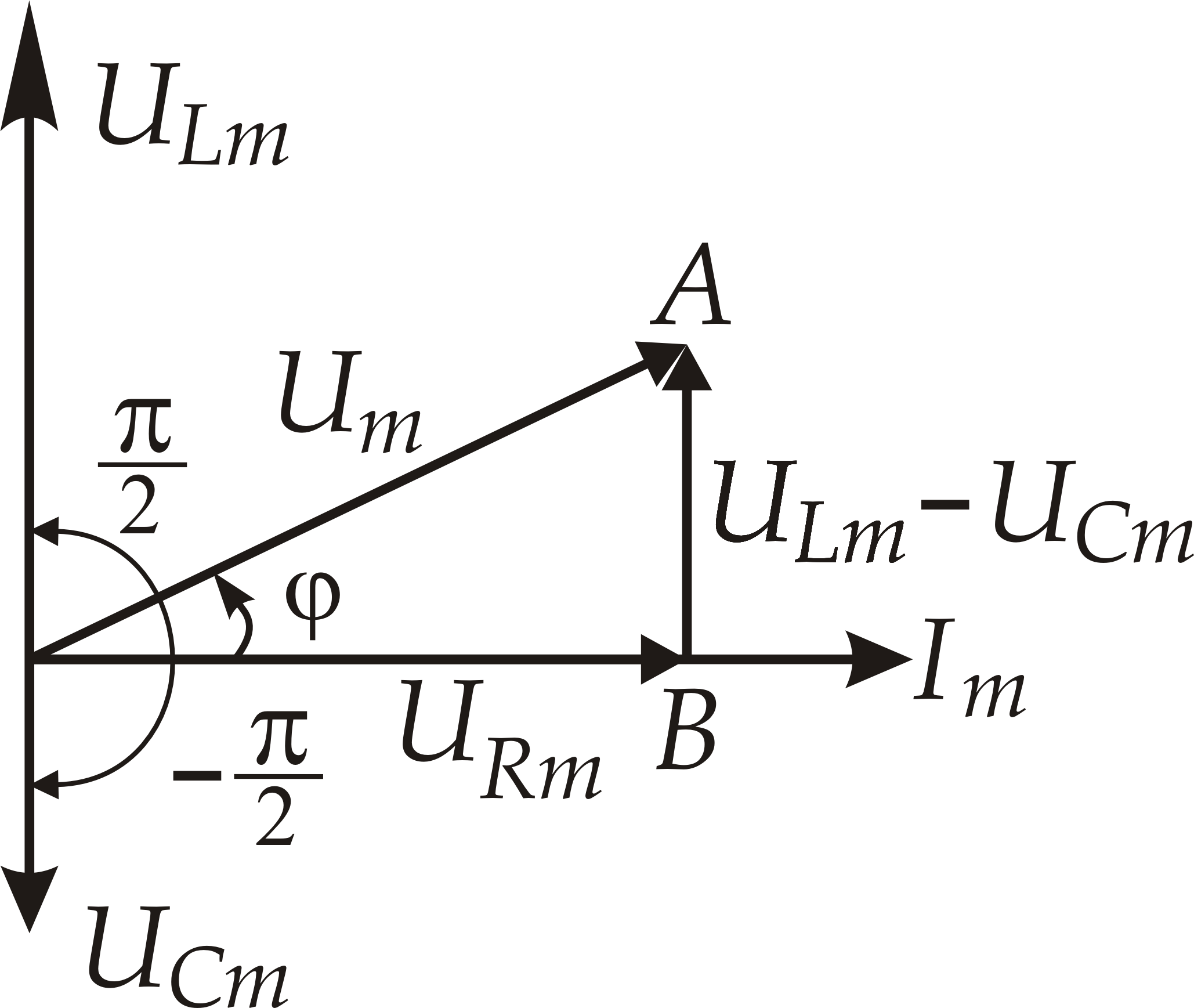
, а напряжение на индуктивности 
, напряжение на емкости — 
.
Выведем закон Ома для рассматриваемой цепи. Так как модуль вектора UL + UC рассчитывают как разность действующих значений UL–UC,
то из диаграммы следует, что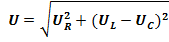 
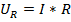
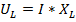
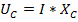
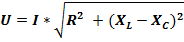
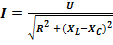
. Но 
; 
, 
; следовательно, 
,откуда
.
Введя обозначение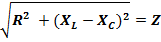 
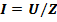
,где Z–полное сопротивление цепи, найдем, что полный ток рассматриваемой цепи определится как:
.
Разность между индуктивным и емкостным сопротивлениями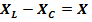 
называют реактивным сопротивлением цепи.
43. Треугольники сопротивлений и мощности в неразветвленной цепи. Резонанс напряжений. 
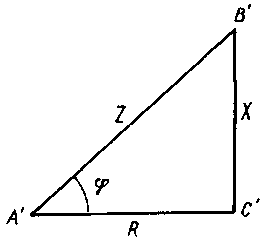
Если каждую сторону треугольника напряжений разделим на ток I, получим подобный треугольник со сторонами, дающими в масштабе полное Z, активное R и реактивное X сопротивления последовательной цепи – треугольник сопротивлений:
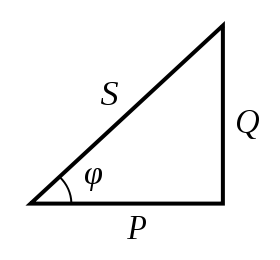
Если же каждую сторону треугольника напряжений умножим на ток I, то получим также подобный треугольник со сторонами, дающими в масштабе полную мощность S, активную P и реактивную Q мощности последовательной цепи, т.е. получим треугольник мощностей этой последовательной электрической цепи (см. рисунок ниже).
Графическое представление электрических мощностей.
Резонанс напряжений.
Резонансом напряжений называют явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника. Условием резонанса напряжений является равенство Х = 0 или ХL = XC , здесь X – результирующее реактивное сопротивление последовательной электрической цепи. Но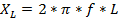 
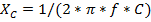
, а 
, где f– частота источника питания. В результате можно записать
Решив это уравнение относительно f, получим значение частоты, при которой наступает резонанс напряжений в этой цепи:
.
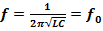
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Электрическая цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром.
Принимаем фазу тока нулевой, т.е. ток в этой цепи изменяется по закону: .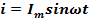
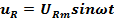
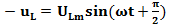
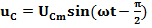
Тогда напряжение на активном сопротивлении будет изменяться как , а напряжение на индуктивности , напряжение на емкости — .
Выведем закон Ома для рассматриваемой цепи. Так как модуль вектора UL + UC рассчитывают как разность действующих значений UL–UC,
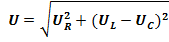
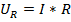
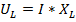
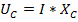
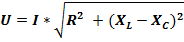
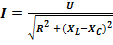
то из диаграммы следует, что . Но ; , ; следовательно, ,откуда
.
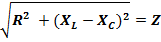
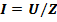
Введя обозначение ,где Z–полное сопротивление цепи, найдем, что полный ток рассматриваемой цепи определится как:
.
Разность между индуктивным и емкостным сопротивлениями 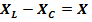называют реактивным сопротивлением цепи.
43. Треугольники сопротивлений и мощности в неразветвленной цепи. Резонанс напряжений.
Если каждую сторону треугольника напряжений разделим на ток I, получим подобный треугольник со сторонами, дающими в масштабе полное Z, активное R и реактивное X сопротивления последовательной цепи – треугольник сопротивлений:
Если же каждую сторону треугольника напряжений умножим на ток I, то получим также подобный треугольник со сторонами, дающими в масштабе полную мощность S, активную P и реактивную Q мощности последовательной цепи, т.е. получим треугольник мощностей этой последовательной электрической цепи (см. рисунок ниже).
Графическое представление электрических мощностей.
Резонанс напряжений.
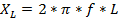
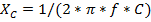
Резонансом напряжений называют явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника. Условием резонанса напряжений является равенство Х = 0 или ХL = XC , здесь X – результирующее реактивное сопротивление последовательной электрической цепи. Но , а , где f– частота источника питания. В результате можно записать
Решив это уравнение относительно f, получим значение частоты, при которой наступает резонанс напряжений в этой цепи:
.
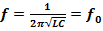
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Неразветвленная цепь обладает активным сопротивлением R и индуктивностью L и подключена к источнику синусоидального напряжения. В соответствии со вторым законом Кирхгофа
где ua и ua uL – активная и индуктивная составляющая напряжения, В
Напряжение опережает по фазе ток на угол φ. Амплитудное значение входного напряжения
где Uam = Im·R – амплитудное значение активной составляющей напряжения, В; ULm = L·Im·w – амплитудное значение реактивной составляющей напряжения, В.
Действующее значение напряжения
На рис. 2. представлена векторная диаграмма цепи, где напряжения U, Ua, UL образуют треугольник напряжений для активно-индуктивной нагрузки.
 |
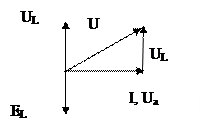Угол сдвига фаз между векторами входного напряжения и тока в цепи определяют из треугольника напряжений
Полное сопротивление цепи (Ом)
I=U/Z
Эта формула выражает закон Ома для действующих значений тока и напряжения цепи с активным сопротивлением и индуктивностью.
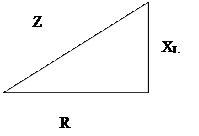
Полное сопротивление цепи Z графически изображают гипотенузой прямоугольного треугольника сопротивлений (рис.3.) , а катетами его являются активное R и индуктивное XL сопротивления в соответствии с выражением (12). Треугольник сопротивлений может быть получен из треугольника напряжений делением всех его сторон на I.
 |
Среднее значение мощности цепи равно среднему значению мощности в активном сопротивлении или активной мощности Р:
P=U·I·cosφ=Ua·I=I 2 ·R
Здесь множитель cos φ– коэффициент мощности. В зависимости от его значении при неизменных токе и входном напряжении активная мощность изменяется от нуля (при φ= π/2) до максимального значения (при φ =0).
QL=U·I·sinφ=UL·I = I 2 ·XL
Произведение действующих значений входного напряжения и тока называют полной мощностью (В·А):
S=U·I
Активную, реактивную и полную мощности изображают сторонами прямоугольного треугольника мощностей (рис. 4), тогда
 |
Неразветвленная цепь переменного тока с активным сопротивлением и емкостью.
Если в цепи с последовательно соединенным резистором и конденсатором проходит ток i = Im sin ωt , то напряжение на активном сопротивлении uа совпадает по фазе с током, а напряжение на конденсаторе uс отстает от тока на угол π/2. Напряжение на зажимах цепи
Амплитуда этого напряжения
Действующее значение напряжения
, или 
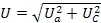
Закон Ома для действующих значений тока и напряжения
где Z — полное сопротивление цепи.
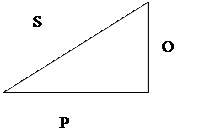
Сопротивления Z, R и XCграфически изображают сторонами треугольника сопротивлений для активно-емкостной нагрузки (рис. 5)
| R |
Активную, реактивную и полную мощности цепи с активным сопротивлением и емкостью и фазовый сдвиг определяют аналогично тому, как это делалось для неразветвленной цепи с индуктивным и активным сопротивлениями. Мощности Р, Q, и S образуют стороны треугольника мощностей. (рис. 6).
 |
| QС |
Неразветвленная цепь переменного тока с активным сопротивлением, индуктивностью и емкостью.
Если в цепи с последовательно соединенными резистором R, индуктивностью L и емкостью С проходит ток i = Im ·sin ωt , то мгновенное значение напряжения на зажимах этой цепи равно сумме мгновенных значений трех составляющих:
Амплитуда этого напряжения
Действующее значение напряжения
где Х=XL — XC— реактивное сопротивление цепи.
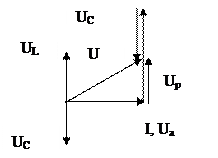
На рис.7 представлены векторная диаграмма и треугольник сопротивлений неразветвленной цепи R L C при XL>XC.
Из векторной диаграммы или треугольника сопротивлений можно определить сдвиг по фазе между напряжением и током
cos φ= Ua/U = R/Z
Активная мощность цепи
P=U·I·cosφ
Q=U·I·sinφ
Полная мощность цепи
 |
 |
| XL |
Резонанс напряжений.
В неразветвленной цепи RLC при равенстве реактивных XL = XC сопротивлений наступает резонанс напряжений:
ω·L= 1/(ω·C),
откуда угловая резонансная частота
Полное сопротивление цепи при резонансе напряжений равно активному сопротивлению и приобретает минимальное значение:
Ток в цепи при постоянстве действующего значения входного напряжения U имеет наибольшее значение и совпадает по фазе с напряжением, т.е. φ=0 и коэффициент мощности cos φ=1.
При резонансе напряжений падения напряжений UL и UC находятся в противофазе, равны между собой UL = UC и приобретают максимальное значение.
Вопросы для самоконтроля
1. Какие значения переменного тока Вы знаете?
2. Что такое фаза, начальная фаза, сдвиг фаз?
3. Как определить отстающую по фазе величину?
4. Что называется векторной диаграммой?
5. Какие элементы цепи обладают активным сопротивлением, а какие реактивным?
6. От каких факторов зависит реактивное сопротивление?
7. Дайте определение активной и реактивной мощности. В чем их различие?
8. Что такое резонанс напряжений? Какими признаками он характеризуется?
Лабораторная работа №3 «Последовательное соединение катушки индуктивности и конденсатора»