Часть II. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Глава тринадцатая. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
§ 13.1. Основные определения.
Как уже говорилось в § 2.1, под нелинейными электрическими цепями принято понимать электрические цепи, содержащие нелинейные элементы. Нелинейные элементы подразделяют на резистивные, индуктивные и емкостные.
Нелинейные резисторы (HP) в отличие от линейных обладают нелинейными вольт-амперными характеристиками. Напомним, что вольт-амперная характеристика (ВАХ) — это зависимость тока, протекающего через резистор, от напряжения на нем. Нелинейные резисторы могут быть подразделены на две большие группы: неуправляемые и управляемые. В управляемых HP в отличие от неуправляемых кроме основной цепи, как правило, есть еще по крайней мере одна вспомогательная или управляющая цепь, воздействуя на ток или напряжение которой можно деформировать ВАХ основной цепи. В неуправляемых HP ВАХ изображается одной кривой, а в управляемых — семейством кривых.
В группу неуправляемых HP входят лампы накаливания, электрическая дуга, бареттер, газотрон, стабиловольт, тиритовые сопротивления, полупроводниковые выпрямители (диоды) и некоторые другие.
В группу управляемых HP входят трехэлектродные (и более) лампы, транзисторы, тиристоры, терморезисторы, фоторезисторы, фотодиоды, магниторезисторы, магнитодиоды, магнитотранзисторы и другие элементы.
© 2019 Научная библиотека
Копирование информации со страницы разрешается только с указанием ссылки на данный сайт
Нелинейные элементы электрических цепей, их вольт-амперные характеристики и сопротивления.
Нелинейным элементом электрической цепи считается элемент, значения параметров которого зависят от значения тока данного элемента или напряжения на его выводах.
К нелинейным элементам электрических целей относятся разнообразные электронные, полупроводниковые и ионные приборы, устройства, содержащие намагничивающие обмотки с ферромагнитными магнитопроводами (при переменном токе), лампы накаливания, электрическая дуга и др.
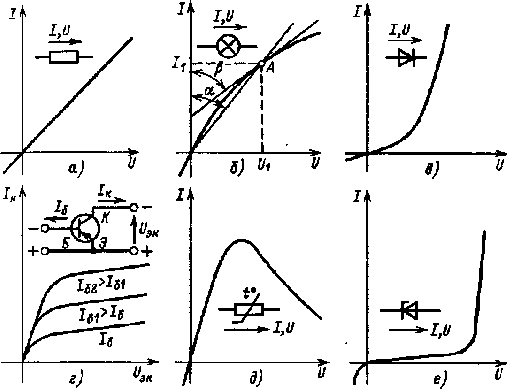
Рис. 1.21. Примеры вольт-амперных характеристик:
а — линейного элемента; б — лампы накаливания; в — полупроводнико- вого диода; г — транзистора (при различных токах базы), д — терморезистора, е – стабилитрона
Нелинейные элементы получают в настоящее время все более широкое распространение, так как они дают возможность решать многие технические задачи. Так, с помощью нелинейных элементов можно осуществить преобразование переменного тока в постоянный, усиление электрических сигналов, генерирование электрических сигналов различной формы, стабилизацию тока и напряжения, изменение формы анналов, вычислительные операции и т д. Нелинейные элементы широко используются в радиотехнических устройствах, в устройствах промышленной электроники, автоматики, измерительной и вычислительной техники.
Важнейшей характеристикой нелинейных элементов является вольт-амперная характеристика (в. а. х.), представляющая собой зависимость между током нелинейного элемента и напряжением на его выводах: I(U) или U(I).
Зависимость между током I и напряжением U любого пассивного элемента электрической цепи подчиняется закону Ома, согласно которому I = U/r. Поскольку у линейных элементов с изменением тока или напряжения сопротивление остается постоянным, их в. а. х. не отличаются от прямой (рис. 1.21, а).
Рис. 1.22 — К расчету электрической цепи с нелинейным элементом графо-аналитическим методом
У нелинейных элементов в. а. х. весьма разнообразны и для некоторых из них даны на рис. 1.21,б — е. Там же приведены условные графические обозначения соответствующих элементов. Общее условное обозначение любого нелинейного резистивного элемента показано на рис. 1.22, а.
Имея в. а. х. нелинейного элемента, можно определить его сопротивления при любых значениях тока или напряжения. Различают два вида сопротивлений нелинейных элементов: статическое и дифференциальное.
Статическое сопротивление дает представление о соотношении конечных значений напряжения и тока нелинейного элемента и определяется в соответствии с законом Ома. Например, для точки А в. а. х. (рис. 1.21,б) статическое сопротивление
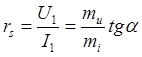
где mu и mi — масштабы напряжения и тока.
Дифференциальное сопротивление позволяет судить о соотношении приращений напряжения и тока и определяется следующим образом:
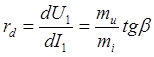
К нелинейным электрическим цепям применимы основные законы электрических цепей, т. е. закон Ома и законы Кирхгофа. Однако расчет нелинейных цепей значительно труднее, чем линейных, Объясняется это тем, что кроме токов и напряжений, подлежащих обычно определению, неизвестными являются также зависящие от них сопротивления нелинейных элементов.
Для расчета нелинейных электрических цепей применяется с большинстве случаев графоаналитический метод. Однако если в предполагаемом диапазоне изменения тока или напряжения нелинейного элемента его в. а. х. можно заменить прямой линией, то расчет можно производить и аналитическим методом.
Следует отметить, что к той части электрической цепи, которая содержит линейные элементы, применимы все методы расчета и преобразования электрических цепей, рассмотренные ранее.
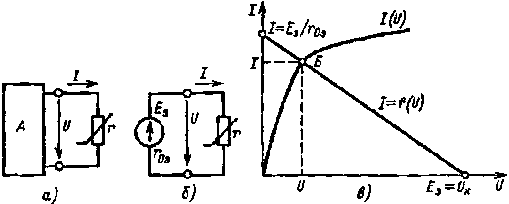
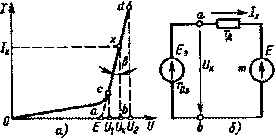
Аналитический метод расчета нелинейных электрических цепей. Предположим, что имеется некоторый нелинейный элемент, в. а. х. которого приведена на рис. 1.26, а. Если данный элемент должен работать на линейном участке cd в.а.х., то для расчета и анализа можно использовать аналитический метод.
Чтобы выяснить зависимость между напряжением и током участка cd и построить схему замещения нелинейного элемента, работающего на данном участке, продлим его до пересечения в точке а с осью абсцисс и будем считать, что в точке пересечения напряжение U равно некоторой ЭДС Е.
Рис. 1.26. К расчету электрической цепи с нелинейным элементом аналитическим методом
Для рис. 1.26, а справедливо следующее очевидное соотношение:
Ob = Oa + ab = Oa + bx tgβ. (1.44)
Выразив в (1.44) отрезки через соответствующие электротехнические величины и масштабы напряжения и тока, получим
После умножения на масштаб напряжения будем иметь
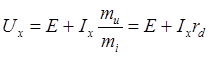
где rd — дифференциальное сопротивление нелинейного элемента на участке cd его в. а. х.
Полученному уравнению (1.45) согласно второму закону Кирхгофа соответствует схема замещения amb (рис. 1.26,б) нелинейного элемента, работающего на линейном участке cd.
Допустим, что нелинейный элемент получает питание от эквивалентного генератора с параметрами Eэ и r0э (рис. 1.26,б), заменяющего некоторый активный двухполюсник. Тогда по второму закону Кирхгофа можно написать
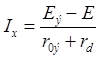
Используя (1.45) и (1.46), нетрудно решать многие задачи, связанные с расчетом и анализом нелинейной электрической цепи. Например, по (1.46) можно определить ток Ix , а по (1.45) — напряжение Ux при заданных Eэ, r0э и rd.
Если графическое определение ЭДС E вызывает затруднение, можно найти ее, воспользовавшись выражением (1.45) и подставив в него известные координаты одной из точек участка cd.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8855 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
1.5.1. Общие сведения
Нелинейная электрическая цепь это электрическая цепь, содержащая один или несколько нелинейных элементов [ 1 ] .
Нелинейный элемент это элемент электрической цепи, параметры которого зависят от определяющих их величин (сопротивление резистивного элемента от тока и напряжения, ёмкость емкостного элемента от заряда и напряжения, индуктивность индуктивного элемента от магнитного потока и электрического тока).
Таким образом, вольт–амперная u ( i ) характеристика резистивного элемента, вебер–амперная ψ( i ) характеристика индуктивного элемента и кулон–вольтная q ( u ) характеристика емкостного элемента имеют вид не прямой линии (как в случае линейного элемента), а некой кривой, обычно определяемой экспериментально и не имеющей точного аналитического представления.
Нелинейная электрическая цепь обладает рядом существенных отличий от линейной и в ней могут возникать специфические явления
1.5. Нелинейные электрические цепи
Рис. 1.28. УГО нелинейных резистивного, индуктивного и емкостного элементов
(например гистерезис), поэтому этого методы расчёта линейных цепей к нелинейным цепям неприменимы. Особо следует отметить неприменимость к нелинейным цепям метода наложения (суперпозиции).
Важно понимать, что характеристики реальных элементов никогда не бывают линейными, однако в большинстве инженерных расчётов они, с допустимой точностью, могут считаться линейными.
Все полупроводниковые элементы (диоды, транзисторы, тиристоры и т. д.) являются нелинейными элементами.
Условные графические обозначения нелинейных резистивного, индуктивного и емкостного элементов приведены на рис. 1.28 . На выносной площадке мажет указываться параметр, вызывающий нелинейность (например температура для терморезистора)
1.5.2. Параметры нелинейных элементов
Нелинейные элементы характеризуются статическими ( R ст , L ст , и C ст ) и дифференциальными ( R д , L д , и C д ) параметрами.
Статические параметры нелинейного элемента определяются как отношение ординаты выбранной точки характеристики к её абсциссе (рис. 1.29 ).
Статические параметры пропорциональны тангенсу угла наклона прямой, проведённой через начало координат и точку, для которой производится расчёт. Для примера на рис. 1.29 получим:
F ст = y A = m y tg α, x A m x
где α–– угол наклона прямой, проведённой через начало координат и рабочую точку A ;
m y и m x –– масштабы по осям ординат и абсцисс соответственно.
1. Основные положения
Рис. 1.29. К определению статических и дифференциальных параметров
F ст = y A , F диф = dy x A dx
Отсюда статические параметры резистивного, индуктивного и емкостного элементов будут иметь следующий вид:
Дифференциальные параметры нелинейного элемента определяются как отношение малого приращения ординаты выбранной точки характеристики к малому приращению её абсциссы (рис. 1.29 ).
Дифференциальные параметры пропорциональны тангенсу угла наклона касательной в рабочей точке характеристики и осью абсцисс. Для примера на рис. 1.29 получим:
F диф = dy = m y tg β, dx m x
где β –– угол наклона касательной в рабочей точке B характеристики и осью абсцисс;
m y и m x –– масштабы по осям ординат и абсцисс соответственно. Отсюда дифференциальные параметры резистивного, индуктив-
ного и емкостного элементов будут иметь следующий вид:
1.5. Нелинейные электрические цепи
1.5.3. Методы расчёта нелинейных цепей
Нелинейность параметров элементов усложняет расчёт цепи, поэтому в качестве рабочего участка стараются выбрать либо линейный, либо близкий к нему участок характеристики и рассматривают, с допустимой точностью, элемент как линейный. Если же это невозможно или нелинейность характеристики является причиной выбора элемента (особенно это характерно для полупроводниковых элементов), то применяют специальные методы расчёта –– графический , аппроксимации
( аналитической и кусочно–линейной ) и ряд других. Рассмотрим эти методы более подробно.
Идея метода состоит в построении характеристик элементов цепи (вольт–амперной u ( i ), вебер–амперной ψ( i ) или кулон–вольтной q ( u )), а затем, путём их графических преобразований (напр. сложения), получения соответствующей характеристики для всей цепи или её участка.
Графический метод расчёта является наиболее простым и наглядным в применении, обеспечивая в основной массе расчётов необходимую точность, однако он применим для небольшого количества нелинейных элементов в цепи и требует аккуратности при проведении графических построений.
Пример расчёта нелинейной цепи графическим методом для последовательного соединения линейного и нелинейного резистивных элементов приведён на рис. 1.30 , а , для параллельного –– на рис. 1.30 , б .
При расчёте последовательной цепи в одних осях строятся характеристики всех рассчитываемых элементов (для рассматриваемого примера это u нэ ( i ) для нелинейного резистора R нэ и u лэ ( i ) для линейного R лэ ). Характер изменения общего напряжения в цепи u ( i ) определяется путём сложения характеристик нелинейного u нэ ( i ) и линейного u лэ ( i ) элементов u ( i ) = u нэ ( i ) + u лэ ( i ). Сложение производится при одинаковых значении тока (для i = i 0 : u 0 = u нэ 0 + u лэ 0 , см. рис. 1.30 , а .).
Расчёт параллельной цепи производится аналогично, только характеристика всей цепи строится путём сложения токов, при постоянном напряжении (для u = u 0 : i 0 = i нэ 0 + i лэ 0 , см. рис. 1.30 , б .).