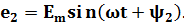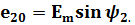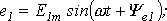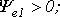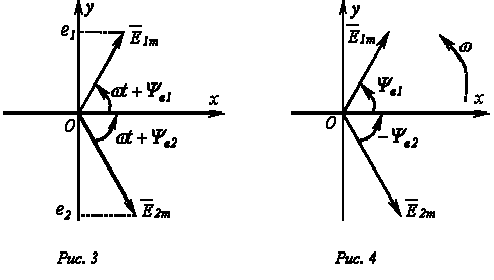Мгновенное амплитудное и действующее значение переменного тока

Что ты хочешь узнать?

Ответ

Проверено экспертом

Речь идём о переменном токе.

Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.

Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :

Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):

Обозначается действующее значение или без иднекса или с индексом «д»:

(только русское «д»).

Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении

Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.

Среднее значение величин (-//-) -среднее арифметическое значение величины за полпериода.

Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.

Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Если ток изменяется по закону синуса, т. е.

,

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:

.

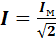
Аналогично для действующих значений синусоидальных напряжений:

.

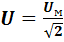
Фаза. Сдвиг фаз.

Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды E_m, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.

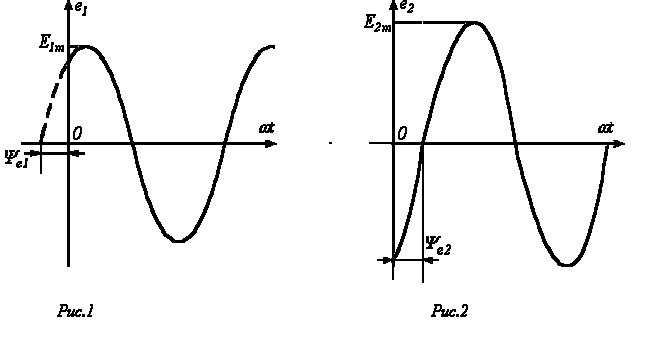
Положение витков задано углами ψ₁ и ψ₂ для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:

;

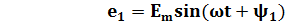
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:

;

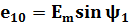
Электрические углы ψ₁ и ψ₂ характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.

Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.

Дата добавления: 2016-05-25 ; просмотров: 7354 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

,

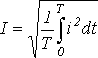
Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

.

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и —начальной фазой ( ).

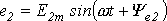
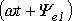
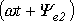
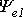
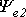
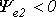
Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

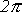
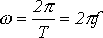
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

.

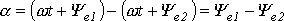
Векторное изображение синусоидально изменяющихся величин

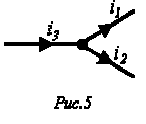
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

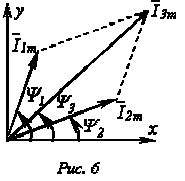
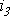
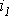
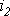
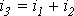
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

.

Каждый из этих токов синусоидален и может быть представлен уравнением

и.

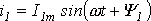
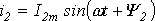
Результирующий ток также будет синусоидален:

.

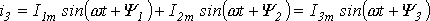
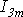
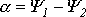
Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

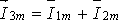
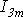
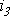
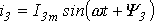
Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.

«>