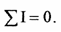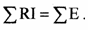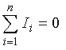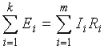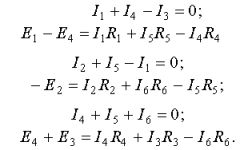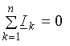Если электрическая цепь с помощью эквивалентных преобразований не сводится к одноконтурной цепи, то для ее расчета используются специальные методы: уравнений Кирхгофа, контурных токов, наложения, узловых потенциалов, эквивалентного генератора. Рассмотрим их.
Самым общим методом расчета электрических цепей является метод уравнении Кирхгофа. Суть его заключается в составлении системы уравнений в соответствии с первым и вторым законами Кирхгофа и решении этой системы относительно неизвестных токов. Система уравнений разрешима, если все входящие в нее уравнения являются линейно независимыми и число уравнений в системе равно числу неизвестных величин. Например, если электрическая цепь имеет у узлов и Ь ветвей, а следовательно, и Ь неизвестных токов, то необходимо составить и решить систему Ь линейно независимых уравнений. Покажем, что эти уравнения можно составить по первому и второму законам Кирхгофа.
По первому закону Кирхгофа можно составить столько уравнений, сколько узлов имеет электрическая цепь, т.е. у уравнений. Однако линейно независимыми будут только у — 1 уравнения. Покажем это на примере.
Составим уравнения по первому закону Кирхгофа для электрической схемы, у которой четыре узла и шесть ветвей (рис. 2.19).
Произвольно выберем направления токов в ветвях; тогда для первого узла / — К — 4 = 0, для второго К + А — /3 = 0, для третьего /6 + /3 — /4 = 0, для четвертого /4 — /| — /5 = 0. Сложив первые три уравнения, получим — /4 + /| + /5 = 0. Умножим это уравнение на — 1. Тогда уравнение для четвертого узла можно получить линейными комбинациями из уравнений, составленных по первому закону Кирхгофа для первых у — 1 узлов.
Видно, что одно из уравнений системы, составленное по числу узлов, является зависимым. Поэтому по первому закону Кирхгофа составляется только у — 1 уравнение, т.е. на одно меньше, чем число узлов в электрической цепи. Так как в схеме четыре узла, то число уравнений, которые составляются по первому закону Кирхгофа, равно трем. Остальные п = Ь — (у — 1) линейно независимых уравнений составляются по второму закону Кирхгофа. Для рассматриваемой схемы п = 6 — (4 — 1) = 3.
Таким образом, для электрической цепи, содержащей у узлов и Ь ветвей, по второму закону Кирхгофа можно составить п = Ь — (у — 1) линейно независимых уравнений. При этом общее число уравнений, составленных по первому и второму законам Кирхгофа, будет равно числу ветвей электрической цепи.
Расчет электрических цепей с помощью законов Кирхгофа целесообразно проводить в следующем порядке.
- 1. Определить число узлов у и число ветвей Ь в электрической цепи. В соответствии с этим найти количество уравнений, которые необходимо составить по первому и второму законам Кирхгофа.
- 2. Обозначить на схеме цепи токи в ветвях и произвольно выбрать их направления. Выбрать независимые замкнутые контуры электрической цепи таким образом, чтобы в каждый контур, во-первых, входило возможно меньшее число ветвей и, во-вторых, чтобы в каждый последующий контур входила хотя бы одна новая ветвь. Произвольно задаться направлением обхода контуров.
- 3. Составить)’ — 1 уравнение по первому закону Кирхгофа. При этом считать положительными токи, входящие в узел, а отрицательными — выходящие из узла, или наоборот.
- 4. Составить п = Ь — (у — 1) уравнений по второму закону Кирхгофа. В этих уравнениях значение ЭДС берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура. Падения напряжений на сопротивлениях в замкнутом контуре электрической цепи берутся со знаком «+», если направление обхода контура совпадает с выбранным направлением тока, и со знаком «-», если не совпадает.
- 5. Решить составленную систему уравнений относительно неизвестных токов. Если при этом некоторые токи получаются отрицательными, это означает, что их действительные направления противоположны произвольно выбранным. Направления этих токов на схеме обратные.
- 6. Проверить правильность решения задачи путем составления уравнения баланса мощности.
Пример 2.4. В электрической цепи (рис. 2.20) Е =50 В, ?3 = 10 В, Гц = 0,4 Ом, г,2 = 1 Ом, /*| = 3 Ом, /’2 = г у = 2 Ом. Требуется определить токи в ветвях.
Решение. В схеме два узла и три ветви. Следовательно, по первому закону Кирхгофа необходимо составить одно уравнение, а по второму — два. Обозначим на схеме электрической цепи узлы, токи в ветвях и стрелками произвольно укажем их положительные направления. Выберем два независимых контура и стрелками покажем направления их обхода. Составим уравнение по первому закону Кирхгофа для первого узла: /( + Л, — /3 = 0 .
Составим уравнения по второму закону Кирхгофа для выбранных независимых контуров:
Полученные уравнения образуют систему независимых уравнений с тремя неизвестными:
Решив эту систему, будем иметь: 1 = 10 А, /2 = —2А, /3 = 8 А. По полученным знакам токов устанавливаем, что действительные направления токов 1 и /3 совпадают, а тока /2 — противоположно произвольно выбранным положительным направлениям.
Правильность расчета токов проверяют по балансу мощностей.
При расчете электрических цепей с помощью законов Кирхгофа источники электрической энергии, заданные в виде источника тока, должны учитываться при составлении уравнений по первому закону Кирхгофа.
Недостатком рассмотренного метода расчета электрических цепей является его громоздкость (число уравнений равно числу ветвей).
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:
Согласно второму закону Кирхгофа алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.
Расчет многоконтурной линейной электрической цепи, имеющей «b» ветвей с активными и пассивными элементами и «у» узлов, сводится к определению токов отдельных ветвей и напряжений на зажимах элементов, входящих в данную цепь.
Пассивной называется ветвь, не содержащая источника ЭДС. Ветвь, содержащая источник ЭДС, называется активной.
1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (y — I) уравнений.
Недостающие уравнения в количестве b — (у — I) составляют, исходя из второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.
Порядок выполнения расчета:
- выделяют в электрической цепи ветви, независимые узлы и контуры;
- с помощью стрелок указывают произвольно выбранные положительные направления токов в отдельных ветвях, а также указывают произвольно выбранное направление обхода контура;
- составляют уравнения по законам Кирхгофа, применяя следующее правило знаков:
- токи, направленные к узлу цепи, записывают со знаком «плюс», а токи, направленные от узла,- со знаком «минус» (для первого закона Кирхгофа);
- ЭДС и напряжение на резистивном элементе (RI) берутся со знаком»плюс», если направления ЭДС и тока в ветви совпадают с направлением обхода контура, а при встречном направлении — со знаком «минус»;
Отрицательные значения тока какой-либо ветви указывают на то, что выбранные ранее произвольные направления тока оказались ошибочными. Это следует учитывать, например, при построении потенциальной диаграммы, где следует знать истинное направление тока.
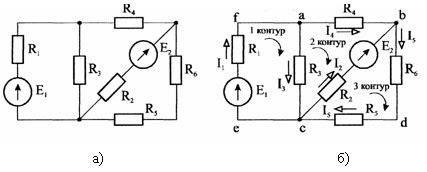
На рис. 4, а изображена исходная электрическая схема, для которой следует рассчитать токи в ветвях. Направления токов и обхода контуров приведены на рис. 4, б.
Система уравнений, составленных по первому и второму законам Кирхгофа, имеет вид
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.
Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
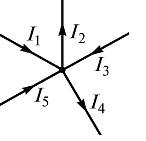
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0
В этом уравнении токи, направленные к узлу, приняты положительными.
Физически первый закон Кирхгофа – это закон непрерывности электрического тока.
Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
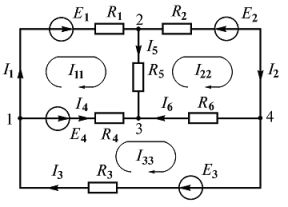
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.
Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4
Замечание о знаках полученного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.
Расчет разветвленной электрической цепи с помощью законов Кирхгофа
Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.
Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.
Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.
Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b — (y — 1) = b — y +1 .
Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.
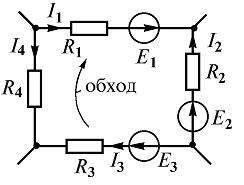
Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.
Поэтому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.
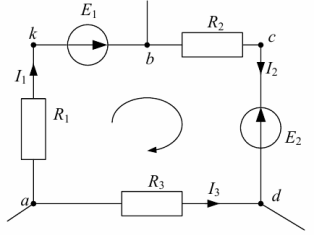
Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.
Составляем необходимое число уравнений по первому и второму законам Кирхгофа
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.
Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.
Рис. 4. Контур для построения потенциальной диаграммы
Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а — I1R1 , ? b = ? к + Е1, ?с = ? b — I2R2 , ? d = ?c — Е2, ? a = ?d + I3R3 = 0
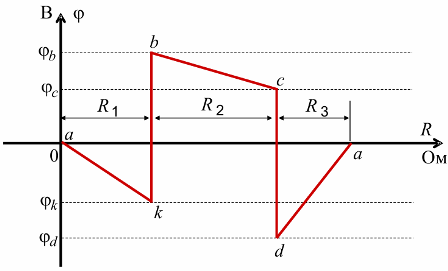
При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).
Рис. 5. Потенциальная диаграмма
Законы Кирхгофа в комплексной форме
Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.
Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»
Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».