Логическая функция исключающее или

Операция исключающее ИЛИ (неравнозначность, сложение по модулю два) обозначается символом и отличается от логического ИЛИ только приA=1 и B=1.

Таким образом, неравнозначность двух высказываний Х1 и Х2 называют такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.

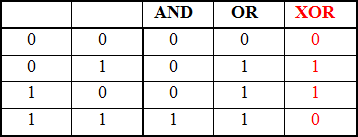
Определение данной операции может быть записано в виде таблицы истинности (таблица 6):

Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Как видно из таблицы 6, логика работы элемента соответствует его названию.

Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.

Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.

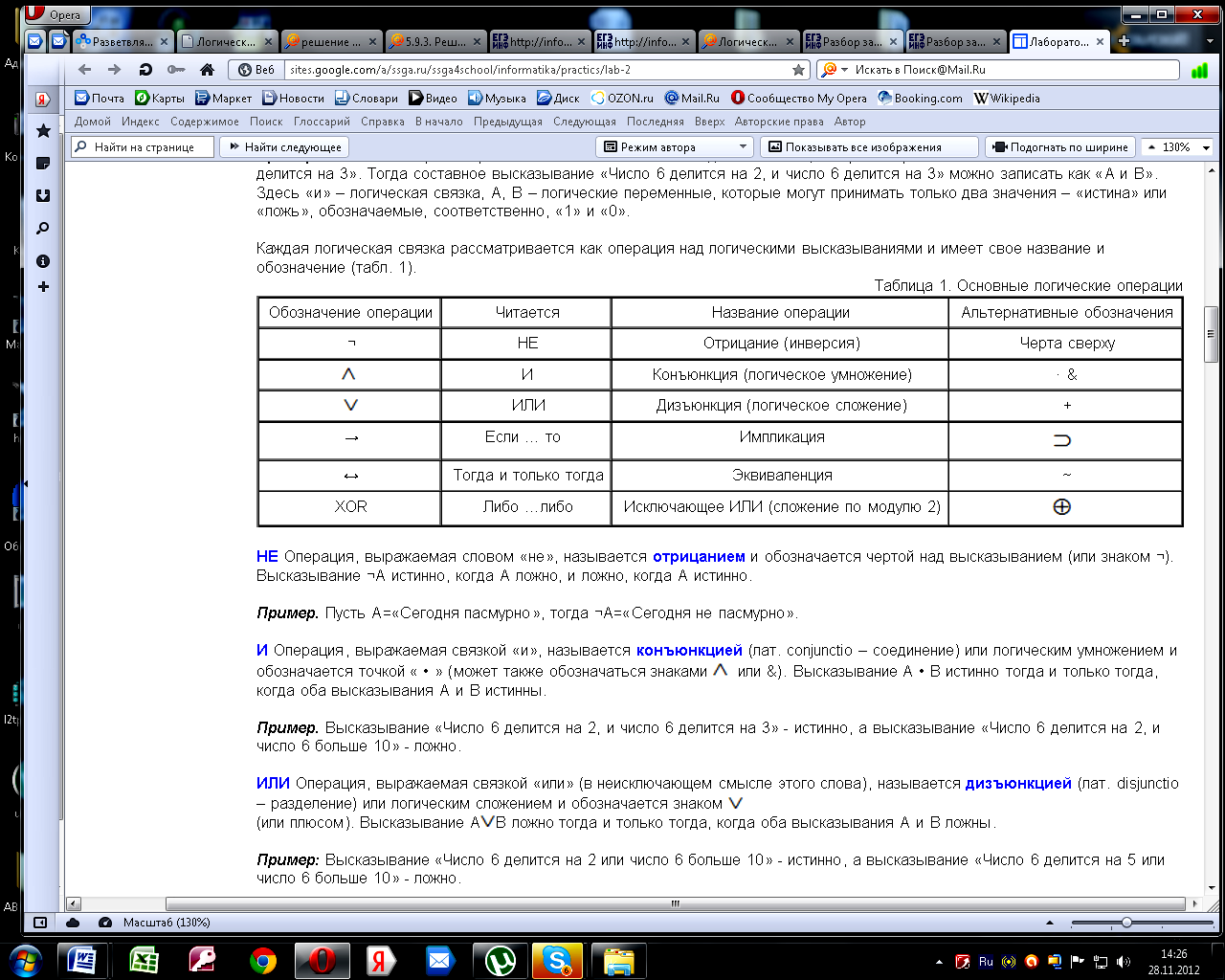
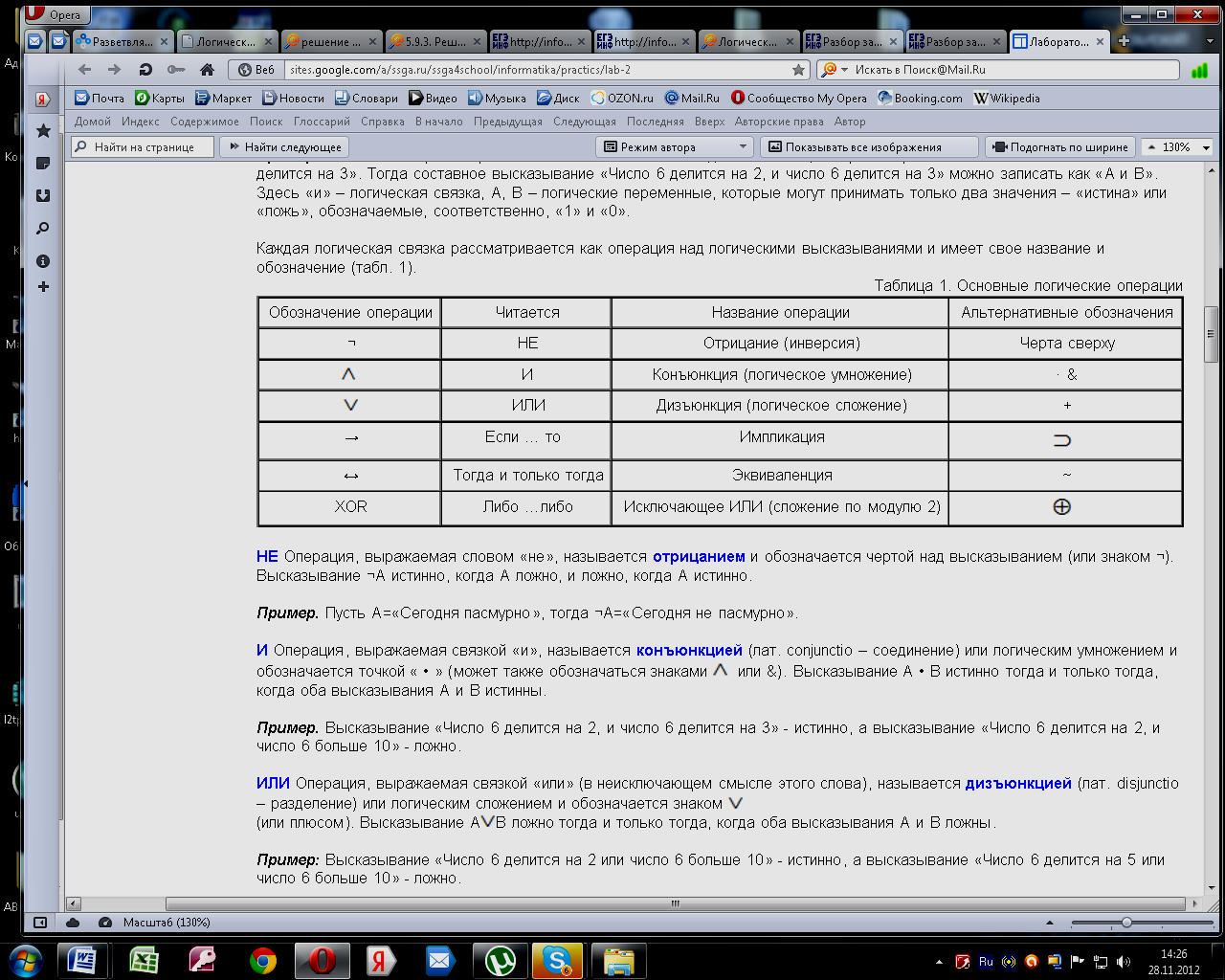
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).

Таблица 7 – Основные логические операции

Конъюнкция (логическое умножение)

Дизъюнкция (логическое сложение)

Тогда и только тогда

ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2)

Порядок выполнения логических операций в сложном логическом выражении

Система логических операций инверсии, конъюнкции, дизъюнкции позволяет построить сколь угодно сложное логическое выражение.

При вычислении значения логического выражения принят определённый порядок выполнения логических операций.

Для изменения указанного порядка выполнения операций используются скобки.

Логические выражения и таблицы истинности

Логические выражения

Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.

Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Запишем в форме логического выражения составное высказывание «(2·2=5 или 2∙2=4) и (2∙2≠5 или 2∙2≠4)».

Проанализируем составное высказывание. Оно содержит два простых высказывания:

В = «2•2=4»—истинно (1).

Тогда составное высказывание можно записать в следующей форме:

«(А или В) и (Ā или В)».

Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:

инверсия, конъюнкция, дизъюнкция.

Для изменения указанного порядка могут использоваться скобки:

F = (A v В) & (Ā v В).

Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.

Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:

F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.

Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.

Простые высказывания обозначаются переменными (например, A и B).

При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:

необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:

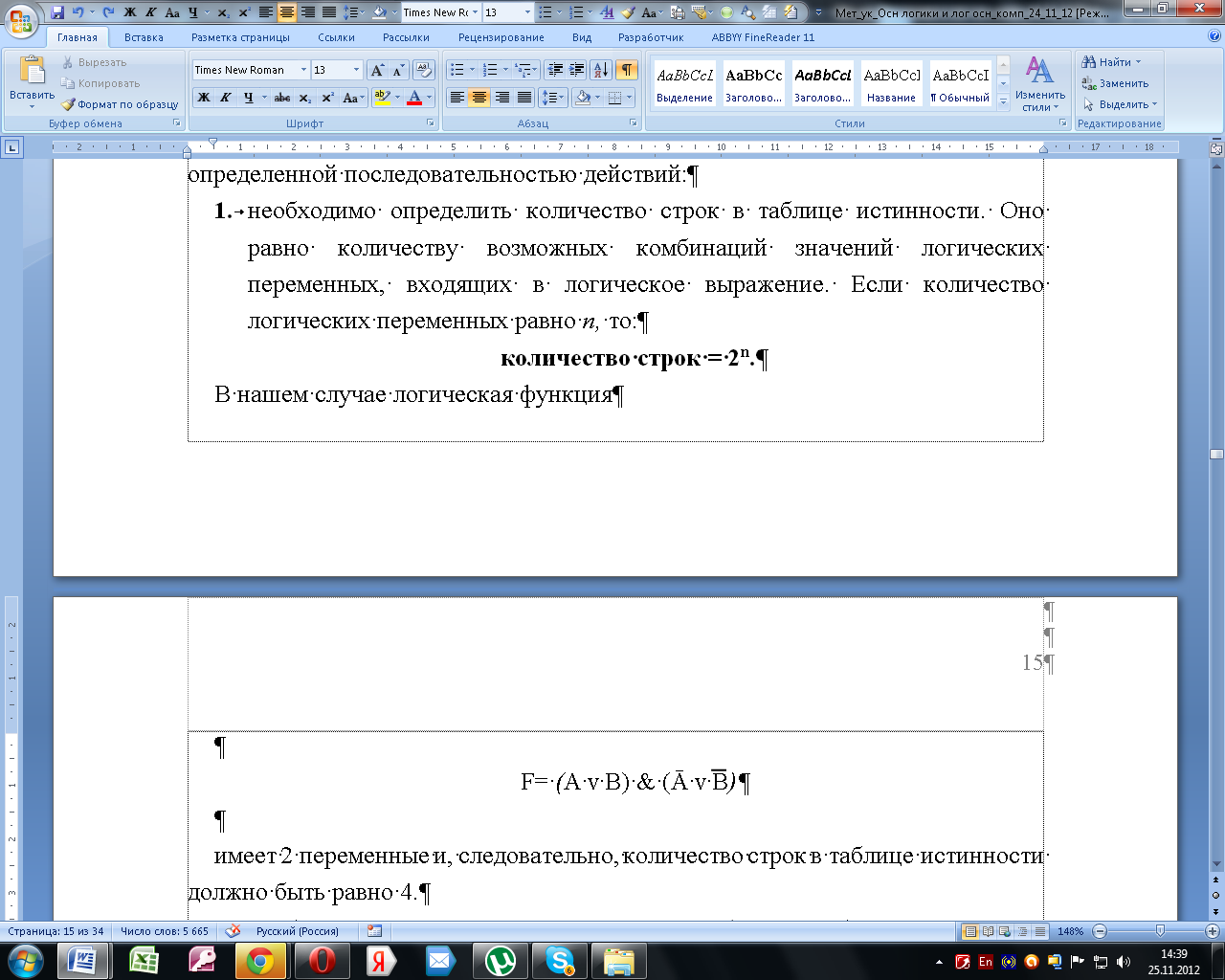
В нашем случае логическая функция

имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;

необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;

необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;

необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.

Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

Таблица 8 – Таблица истинности логической функции

В данной статье я расскажу о битовой операции XOR (исключающее ИЛИ) и приведу наиболее интересные примеры ее применения на JAVA.

Итак, XOR – операция, которая принимает значение «истина» только если всего один из аргументов имеет значение «истина».

XOR обладает следующими свойствами:

a XOR 0 = a
a XOR a = 0
a XOR b = b XOR a
(a XOR b) XOR b = a

В языке JAVA (а также в С, С++, C#, Ruby, PHP, JavaScript) операция обозначается символом «^».

Обмен значений переменных без использования дополнительной переменной

С использованием операции XOR можно реализовать обмен значений однотипных пременных без использования дополнительной переменной:

или в более короткой записи:

Таким образом можно, например, реализовать реверс текстовой строки:

Следует, однако, заметить, что такой код не дает выигрыша в скорости по сравнению с кодом использующим временную переменную.

Шифрование

Шифрование на основе операций XOR использует свойство:
(a XOR k) XOR k = a
где k – выступает в роли ключа

Простая реализация шифрования строки:

Попробуем зашифровать строку “Съешь ещё этих мягких французских булок, да выпей чаю.” И в качестве ключа возьмем слово “хабра”:

Узким местом такого шифрования является то, что зная часть зашифрованного текста можно с легкостью восстановить ключ и, соответственно, разшифровать весь текст. Поэтому в чистом виде он редко используется на практике, хотя его применяют как часть более сложных алгоритмов шифрования.
Интересно, что в свое время данный алгоритм использовался Microsoft для шифрования содержимого документов в Office 95.

Генератор случайных чисел XORShift

В 2003 году Джордж Марсаглия представил миру быстрый алгоритм генерации случайных чисел с использованием XOR – XORShift.

Одна из возможных его рализаций:

Тут “магические“ числа 21, 35 и 4 подобраны для генерации лучшей последовательности (полный период равен 2 64 -1).
Проинициализировав генератор числом 1111111111, получим такую последовательность для первых 10 чисел:

39462749392662495
4596835458788324745
-7932128052244037525
-2502212788642280052
3288035714308340525
-8561046377475020727
-812160615072319265
-3869866974339671508
-7329504029400927428
3890915262874757420

В заключение просьба тем, у кого есть другие красивые примеры применения XOR, не вошедшие в статью, рассказать о них.

Операция исключающее ИЛИ (неравнозначность, сложение по модулю два) обозначается символом и отличается от логического ИЛИ только приA=1 и B=1.

Таким образом, неравнозначность двух высказываний Х1 и Х2 называют такое высказывание Y, которое истинно тогда и только тогда, когда одно из этих высказываний истинно, а другое ложно.

Определение данной операции может быть записано в виде таблицы истинности (таблица 6):

Таблица 6 – Таблица истинности операции «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Как видно из таблицы 6, логика работы элемента соответствует его названию.

Это тот же элемент «ИЛИ» с одним небольшим отличием. Если значение на обоих входах равно логической единице, то на выходе элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ», в отличие от элемента «ИЛИ», не единица, а ноль.

Операция «ИСКЛЮЧАЮЩЕЕ ИЛИ» фактически сравнивает на совпадение два двоичных разряда.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет своё название и обозначение (таблица 7).

Таблица 7 – Основные логические операции

Конъюнкция (логическое умножение)

Дизъюнкция (логическое сложение)

Тогда и только тогда

ИСКЛЮЧАЮЩЕЕ ИЛИ (сложение по модулю 2)

Порядок выполнения логических операций в сложном логическом выражении

Система логических операций инверсии, конъюнкции, дизъюнкции позволяет построить сколь угодно сложное логическое выражение.

При вычислении значения логического выражения принят определённый порядок выполнения логических операций.

Для изменения указанного порядка выполнения операций используются скобки.

Логические выражения и таблицы истинности

Логические выражения

Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.

Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Запишем в форме логического выражения составное высказывание «(2·2=5 или 2∙2=4) и (2∙2≠5 или 2∙2≠4)».

Проанализируем составное высказывание. Оно содержит два простых высказывания:

В = «2•2=4»—истинно (1).

Тогда составное высказывание можно записать в следующей форме:

«(А или В) и (Ā или В)».

Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:

инверсия, конъюнкция, дизъюнкция.

Для изменения указанного порядка могут использоваться скобки:

F = (A v В) & (Ā v В).

Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.

Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:

F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.

Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.

Простые высказывания обозначаются переменными (например, A и B).

При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:

необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:

В нашем случае логическая функция

имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;

необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;

необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;

необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.

Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

Таблица 8 – Таблица истинности логической функции